立方和（差）公式

在数学中，立方和公式和立方差公式是用来分解两个数的立方和或差的等式。这些公式可以帮助简化多项式的运算，尤其是在解代数方程或进行因式分解时。这里是具体的公式：

1. 立方和公式（Cube Sum Formula）:

   $$a^3+b^3=(a+b)(a^2-ab+b^2)$$

   这个公式表明，两个数的立方和可以分解为一个线性因子和一个二次因子的乘积。

2. 立方差公式（Cube Difference Formula）:

   $$a^3-b^3=(a-b)(a^2+ab+b^2)$$

   这个公式说明，两个数的立方差也可以分解为一个线性因子和一个二次因子的乘积。

这些公式在进行立方数的加减运算时非常有用，特别是在解决涉及多项式的问题时，如因式分解、求解多项式方程等。

[2011年1月]已知$x^2+y^2=9,xy=4$,则$\frac{x+y}{x^3+y^3+x+y}=().$

$\begin{array}{rl}& \text{A.}\frac{1}{2}\\ & \text{C.}\frac{1}{6}\\ & \text{E.}\frac{1}{14}\end{array}\text{B.}\frac{1}{5}$

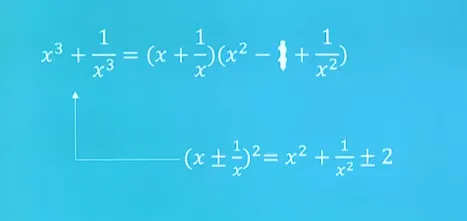
完全立方公式

完全立方公式，也称为立方公式，是一个用于展开三个相同项乘积的公式。如果你想要将一个单项式的三次方展开成多项式的形式，可以使用这个公式。完全立方公式可以分为两种情况：

1. 正的完全立方公式（Perfect Cube Formula for a Positive Term）:

   $$(a+b{)}^3=a^3+3a^{2}b+3a{b}^2+b^3$$

   这个公式展开了 $(a+b)$ 的三次方，并且显示了所有的组合。

2. 负的完全立方公式（Perfect Cube Formula for a Negative Term）:

   $$(a-b{)}^3=a^3-3a^{2}b+3a{b}^2-b^3$$

   这个公式展开了 $(a-b)$ 的三次方，同样显示了所有的组合。

锦囊