什么是指数运算？

指数运算是数学中的一种运算方式，用于表示一个数（底数）自乘若干次的结果。它的基本形式是：

$a^n$

其中，$a$ 是底数，$n$ 是指数，表示 $a$ 自乘 $n$ 次。例如：

• $2^3 = 2 \times 2 \times 2 = 8$
• $5^2 = 5 \times 5 = 25$

在指数运算中，有一些重要的性质：

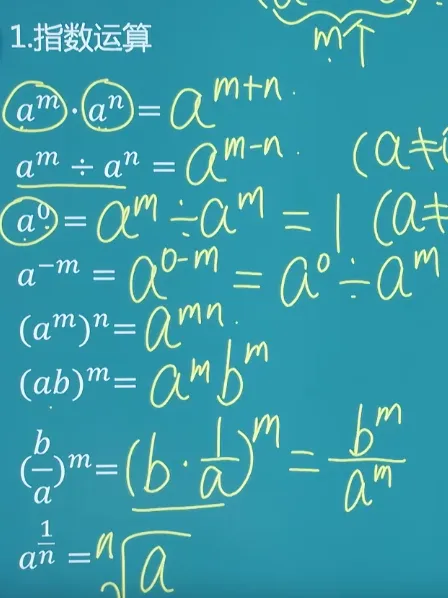
1. 乘法法则：$a^m \times a^n = a^{m+n}$
2. 除法法则：$a^m \div a^n = a^{m-n}$
3. 幂的幂：$(a^m)^n = a^{m \times n}$
4. 零指数：$a^0 = 1$（$a \neq 0$）
5. 负指数：$a^{-n} = \frac{1}{a^n}$（$a \neq 0$）

指数运算在科学、工程和金融等多个领域中都有广泛应用。

指数函数

指数函数是指形如 $f(x) = a^x$ 的函数，其中 $( a )$ 是一个正实数，且 $( a \neq 1 )$。常见的指数函数包括以自然对数的底数 $( e )$ 为底的函数，记作 $( f(x) = e^x )$。

指数函数的性质

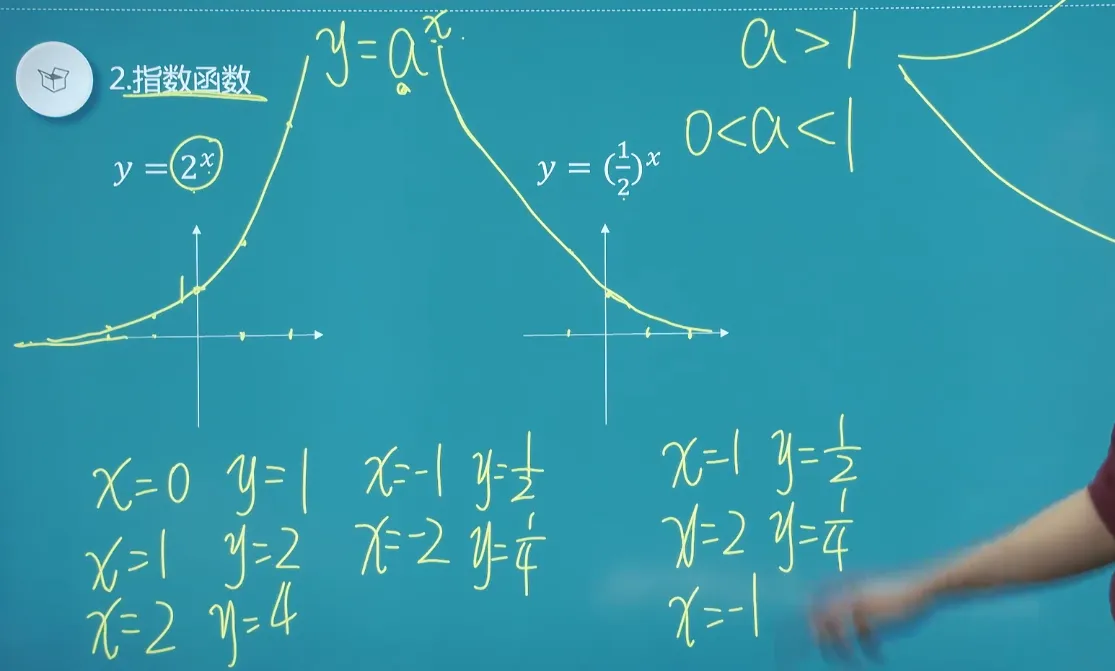
1. 定义域和值域：

   • 定义域：$( (-\infty, +\infty) )$
   • 值域：$( (0, +\infty) )$

2. 单调性：

   • 如果 $( a > 1 )$，则 $( f(x) = a^x )$ 在整个定义域上是递增的。
   • 如果 $( 0 < a < 1 )$，则 $( f(x) = a^x )$ 在整个定义域上是递减的。

3. 图像特征：

   • 当 $( x \to -\infty )$ 时，$( f(x) \to 0 )$。
   • 当 $( x \to +\infty )$ 时，$( f(x) \to +\infty )$。
   • 图像永远不会与 x 轴相交（即没有零点）。

4. 与对数函数的关系：

   • 指数函数与对数函数互为反函数。如果 $( y = a^x )$，则 $( x = \log_a(y) )$。

5. 重要极限：

   • $( \lim_{x \to 0} a^x = 1 )$
   • $( \lim_{x \to \infty} a^x = +\infty )$ （当 $( a > 1 )$

应用

指数函数在许多领域中都有广泛应用，包括：

• 科学：描述自然现象，如放射性衰变、人口增长等。
• 金融：计算复利、投资增长等。
• 工程：信号处理、控制系统等。