勾股定理是三角学中的重要定理,它描述了直角三角形的关系。定理表述如下:
勾股定理:在一个直角三角形中,直角边的平方等于另外两条边的平方和。
数学上可以用公式表示为:
其中


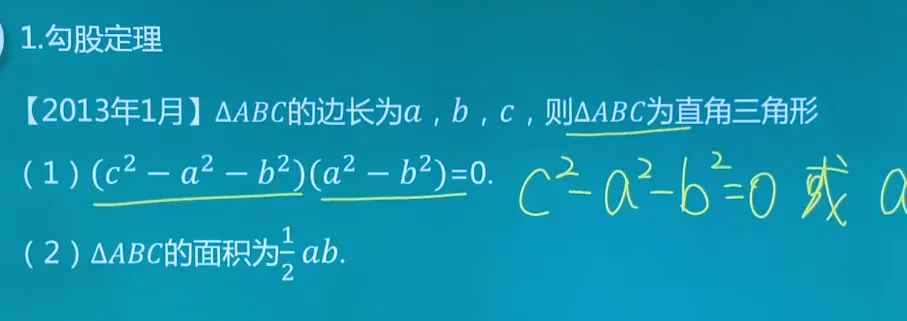
什么是勾股数
勾股数是指一组正整数
其中,
这些数对可以用来构造直角三角形,并且在数学中有广泛的应用。


勾股定理是三角学中的重要定理,它描述了直角三角形的关系。定理表述如下:
勾股定理:在一个直角三角形中,直角边的平方等于另外两条边的平方和。
数学上可以用公式表示为:
其中


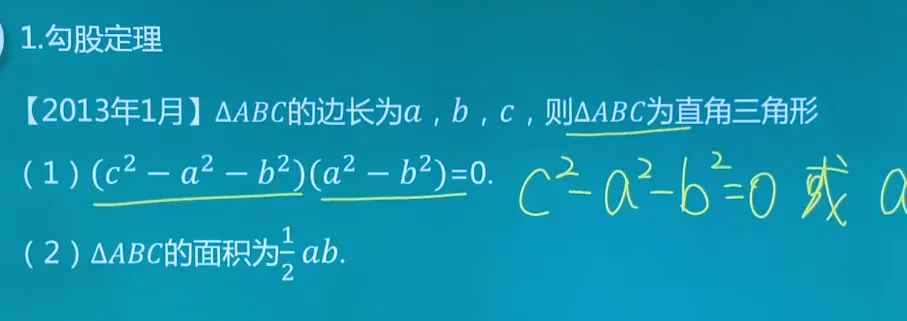
勾股数是指一组正整数
其中,
这些数对可以用来构造直角三角形,并且在数学中有广泛的应用。

