钟文志的部落格

二次公式通常指的是形如 $(ax^2+bx+c=0)$ 的方程，其中 a， b，和 c 是实数系数，而且 $(a\neq0)$ 。这类方程的解可以用求根公式来表示：

这里的 $(b^2-4ac)$ 称为判别式。判别式决定了方程的解的性质：

应用场景

二次公式在生活中可以解决许多与变化、曲线和优化相关的问题。以下是一些示例：

抛物线轨迹问题：当物体在空中自由落体或投掷时，其轨迹可以用二次函数来描述。这对于设计弹道、计算抛物线的最高点和落地点等问题非常有用。
财务规划：二次函数可以用来模拟某些投资或债务的增长或减少趋势。例如，可以使用二次函数来预测股票价格的变化，或者计算债务的偿还计划。
工程设计：在工程设计中，需要考虑各种因素如成本、效率、材料用量等。二次函数可以用来优化这些因素，例如最小化成本或最大化效率。
自然科学：在物理学、化学和生物学等领域，许多现象可以通过二次函数来描述。例如，振动系统的运动方程通常是二次的，化学反应速率与浓度之间的关系也可以用二次函数表示。
生活中的决策问题：二次函数在优化问题中非常有用。例如，在某个预算下最大化收益或最小化成本，或者在某些限制条件下优化某种指标。

总的来说，二次公式在生活中的应用范围很广，几乎可以用于任何需要描述变化或优化的情况。

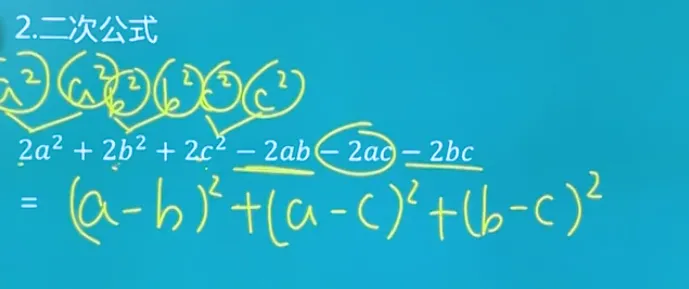
[例2]若ΔABC的三边为 $a,b,c$ 满足 $a^2+b^2+c^2=ab+ac+bc$ ,则 $\Delta ABC$ 为()

A.等腰三角形 B.直角三角形 D.等腰直角三角形 C.等边三角形 E.以上都不是

三个数的完全平方公式是一个数的平方与另外两个数的平方之和加上两倍这两个数的乘积。假设这三个数分别为(a)、(b)和(c)，那么完全平方公式可以表示为：

$[ (a + b + c)^2 = a^2 + b^2 + c^2 + 2ab + 2ac + 2bc ]$

这个公式在展开后可以看作是三个完全平方的和加上一些额外的交叉项。

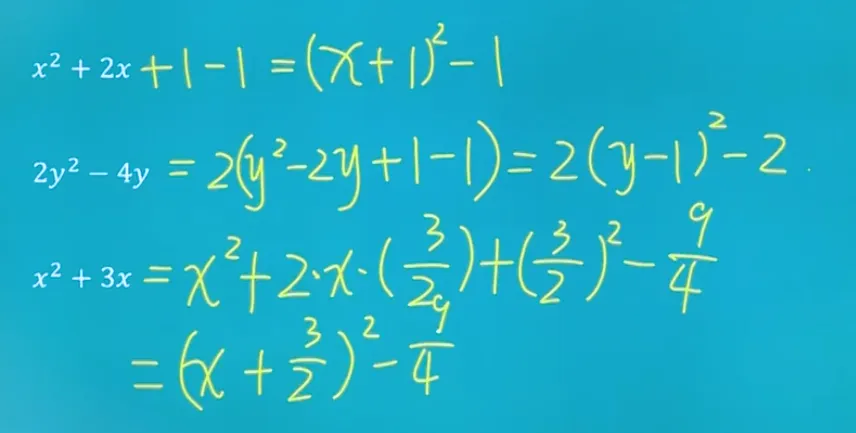
在代数中，“配方法”通常指的是将多项式进行重组和重新排列，以便于进行因式分解或者简化。配方法通常用于解决二次方程、多项式因式分解等问题。

最常见的配方法是针对二次方程的配方法，即将二次项系数前的一项拆分成两个部分，使得可以进行完全平方的操作，从而完成平方的配方法。例如，对于二次方程 $(ax^2 + bx + c = 0)$ ，可以通过配方法将其化为 $((px + q)^2 = 0)$ 的形式。

在多项式因式分解中，配方法指的是将多项式进行重组，以便于找到可以进行因式分解的形式。这可能涉及到提取公因式、分组、使用差分平方公式等方法。

总的来说，配方法是一种将代数表达式重新组织以便于解决问题的方法，常见于解决方程、因式分解等代数运算中。

配方法的一个常见案例是将一个二次项的多项式转化为完全平方的形式。例如，考虑一个简单的二次项多项式 $(x^2 + 6x + 9)$ ，我们可以使用配方法将其转化为完全平方的形式。

将二次项系数的一半加到一次项上，即将 $(6x)$ 中的 $(6)$ 的一半 $(3)$ 加到 $(9)$ 上得到 $(9+3)$ ，同时在 $(x^2 + 6x + 9)$ 中添加 $(3^2)$ （即 $(9)$ ）并减去同样的值，保持等式平衡。这样，原来的多项式就可以写成完全平方的形式：
$[ x^2 + 6x + 9 = (x + 3)^2 ]$

这个过程中，我们实际上是在找到一个完全平方的公式，即 $((x + a)^2 = x^2 + 2ax + a^2)$ ，并将其应用到给定的多项式中。

这种配方法的目的是为了将一个二次项多项式转化为一个更容易处理的形式，从而更容易求解方程或者进行其他的代数运算。

(2012年10月)设实数x，y满足 $x+2y=3$ ,则 $x^2+y^2+2y$ 的最小值为()

$B.5$ $A.4$ $D.\sqrt{5}-1$ $C.6$ E. $\sqrt{5}+1$

完全平方是指一个形式为 $((x + a)^2)$ 的二次多项式，其中 a 是实数。这种形式的多项式可以通过展开得到如下形式：

$[ (x + a)^2 = x^2 + 2ax + a^2 ]$

这里， $(x^2 + 2ax + a^2)$ 是一个完全平方的二次多项式，其中 a 是常数。完全平方的特点是它可以因式分解为两个相同的因子，即 $((x + a)(x + a))$ ，或者写成 $((x + a)^2)$ 的形式。

完全平方常常用于数学中的方程求解、多项式因式分解以及其他代数运算中。通过将一般的二次多项式转化为完全平方的形式，我们可以更容易地分析和解决与这些多项式相关的问题。

通俗的理解为所有数（整体）都被平方了，所以叫完全平方。