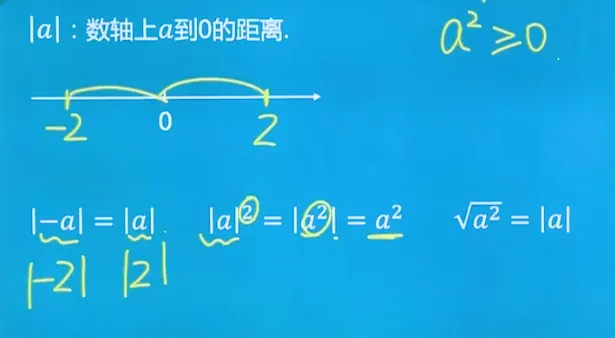
绝对值的几何意义

绝对值在几何上表达了一个数在数轴上到原点的距离。对于实数 $(x)$，其绝对值表示为 $(|x|)$，具体含义取决于 $(x)$ 的正负：

• 如果 $(x)$ 是正数或零，那么 $(|x| = x)$；
• 如果 $(x)$ 是负数，那么 $(|x| = -x)$。

从几何的角度看，可以想象一个数轴，上面有正数和负数以及零点。任何数的绝对值就是它在这个数轴上的位置到零点的直线距离。例如：

• $( |3| = 3 )$，因为 3 在数轴上距离原点的距离是 3；
• $( |-5| = 5 )$，尽管 -5 在数轴上位于原点的左侧，但它到原点的距离仍然是 5。

这种表示方法使得绝对值非常适用于处理距离和大小问题，不考虑方向的影响。在高维空间中，绝对值的概念也可以推广到向量的模长，即向量的长度或大小。例如，在二维或三维空间中，向量的模（或长度）可以通过计算其各分量的平方和的平方根来得到，这与单个数的绝对值类似地表示从原点到该点的距离。