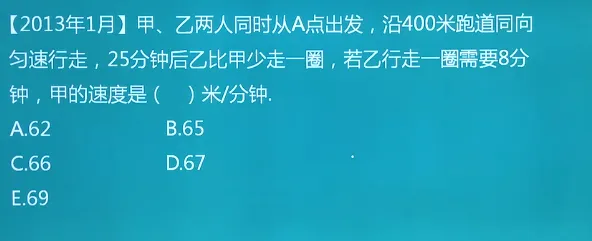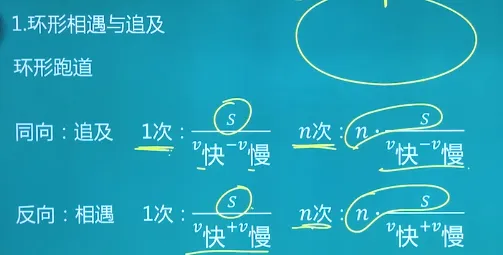
环形相遇和追及是两种不同的情况，分别描述了在环形道路或轨道上的两个物体之间的运动关系。
环形相遇指的是两个物体在环形道路或轨道上同时出发，以相同的速度沿着环形道路或轨道运动，最终在某一点相遇的情况。在环形相遇中，两个物体的速度和运动方向都是相同的，它们在环形道路或轨道上的位置会周期性地重复。
追及则是指一个物体在环形道路或轨道上追赶另一个物体的情况。在追及中，追赶者的速度比被追赶者要快，追赶者会逐渐缩小与被追赶者之间的距离，最终追上被追赶者。
总的来说，环形相遇是两个物体以相同速度在环形道路或轨道上运动并在某一点相遇，而追及是一个物体追赶另一个物体在环形道路或轨道上的情况。
在环形相遇和追及问题中，可以使用以下公式来计算两个物体相遇或追及的情况：
- 环形相遇公式： 假设两个物体在环形道路上以相同的速度$ v 运动，环形道路的周长为 L$，两个物体在环形道路上的起始位置相差为 ，则它们相遇的时间 t 可以通过以下公式计算： 其中， 和 $v2 $分别为两个物体的速度。
- 追及公式： 假设一个物体以速度$ v1 追赶另一个以速度 v2 的物体，它们在环形道路上的起始位置相差为 d$，则它们追及的时间 $t $可以通过以下公式计算：
这些公式可以帮助计算在环形道路上两个物体相遇或追及的时间。需要注意的是，在实际问题中，还需要考虑物体的加速度、转弯半径等因素来更准确地计算。
