"裂项相消"是一种数学技巧，通常用于对一个表达式中的部分项进行加减操作，以简化表达式或证明某个等式成立。

这种技巧常用于处理含有分式的表达式，特别是在证明恒等式或简化复杂表达式时非常有用。

具体来说，裂项相消通常包括以下步骤：

1. 将表达式分解为多个部分项。 这些部分项可能是单项式、多项式或分式。
2. 找到能够相互抵消的部分项。 这些部分项可能在某些方面相反，例如符号相反或者包含相同的因子。
3. 将相消的部分项相加或相减。 这样可以简化表达式，去除不必要的项，使得问题更易于处理。
4. 得到简化后的表达式或证明所需的等式。 通过裂项相消，可以得到更简洁的表达式，或者证明某个恒等式成立。

裂项相消是代数运算中的一种常见技巧，在求解问题和证明定理中都有广泛的应用。

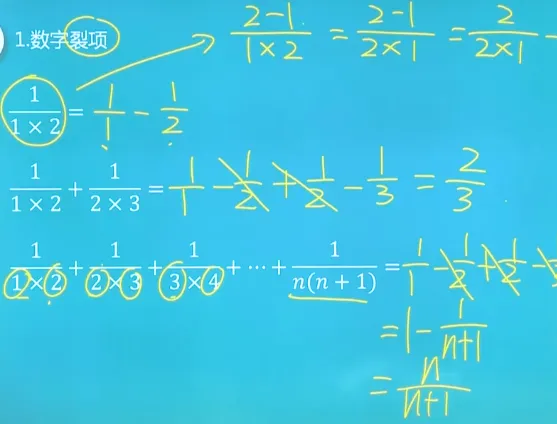
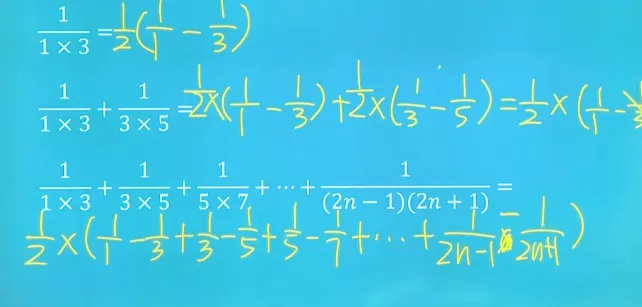
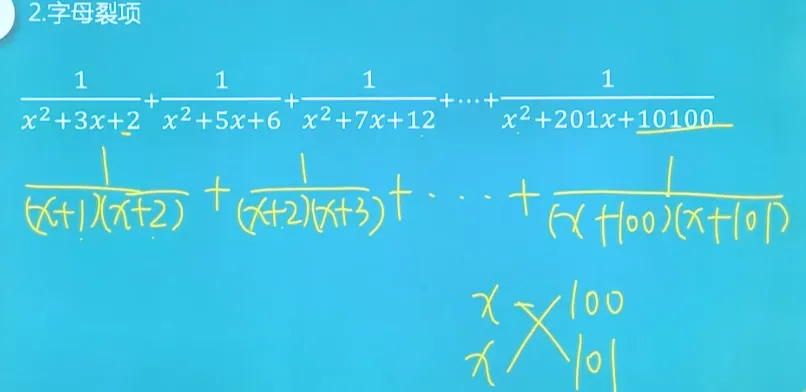
锦囊

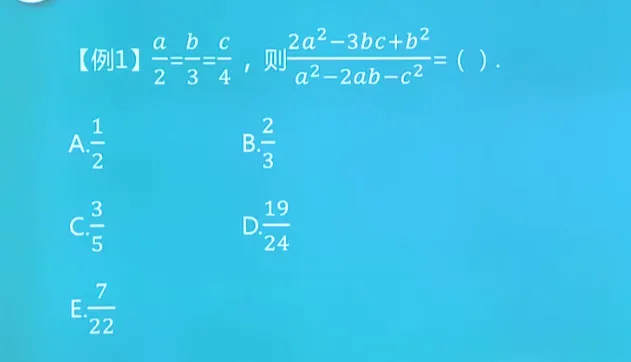
裂项相消是一种求和方法，特别适用于一些特定的数列和。以下是裂项相消法的基本步骤及几个案例：

基本步骤

1. 将每一项进行拆分：将数列中的每一项拆分成两部分，使其相互抵消。
2. 累加后观察相消：将拆分后的项相加，观察相邻项是否可以相消。
3. 计算剩余项：剩下的项即为数列的和。

裂项相消是一种常用于求和的数学方法，尤其在处理一些复杂的级数或求和公式时非常有效。基本思想是通过分解某个项，使得相邻项之间能够相互抵消，最终简化求和过程。

常见的裂项方法

1. 差分裂项法： 这是最常见的一种方法，通过把一个数列的每一项表示为两个数的差，从而使得求和时相邻的项相消。

   案例： 例如，求和 $(\sum _{n=1}^{\mathrm{\infty }}\frac{1}{n(n+1)})$：

   $$\frac{1}{n(n+1)}=\frac{1}{n}-\frac{1}{n+1}$$

   因此，

   $$\sum _{n=1}^{\mathrm{\infty }}\frac{1}{n(n+1)}=\sum _{n=1}^{\mathrm{\infty }}(\frac{1}{n}-\frac{1}{n+1})$$

   这个求和过程中的相邻项会相互抵消，最终结果为：

   $$1-\underset{n\to \mathrm{\infty }}{lim}\frac{1}{n+1}=1$$

2. 分子裂项法： 当分子可以分解为两个部分时，可以采用这种方法。

   案例： 求和 $(\sum _{n=1}^{\mathrm{\infty }}\frac{n}{(n+1)(n+2)})$：

   $$\frac{n}{(n+1)(n+2)}=\frac{(n+2)-1}{(n+1)(n+2)}=\frac{n+2}{(n+1)(n+2)}-\frac{1}{(n+1)(n+2)}$$

   分别计算可以得到：

   $$\frac{n+2}{(n+1)(n+2)}=\frac{1}{n+1},\frac{1}{(n+1)(n+2)}=\frac{1}{n+1}-\frac{1}{n+2}$$

   最终求和式可以写为：

   $$\sum _{n=1}^{\mathrm{\infty }}(\frac{1}{n+1}-(\frac{1}{n+1}-\frac{1}{n+2}))$$

   经过相消，最终结果为：

   $$\sum _{n=1}^{\mathrm{\infty }}\frac{1}{n+2}=\text{无穷大}（\mathrm{因}\mathrm{此}\mathrm{项}\mathrm{不}\mathrm{收}\mathrm{敛}）$$

3. 分母裂项法： 这种方法适用于分母可以分解为若干简单因子的情况。

   案例： 求和 $(\sum _{n=1}^{\mathrm{\infty }}\frac{1}{n^2-1})$：

   $$\frac{1}{n^2-1}=\frac{1}{(n-1)(n+1)}=\frac{1}{2}(\frac{1}{n-1}-\frac{1}{n+1})$$

   求和：

   $$\frac{1}{2}\sum _{n=2}^{\mathrm{\infty }}(\frac{1}{n-1}-\frac{1}{n+1})$$

   经过相消，最终结果为：

   $$\frac{1}{2}(1+\frac{1}{2})=\frac{3}{4}$$

总结

裂项相消法是一种通过将复杂的和式项分解为可相消的部分，从而简化求和的强有力工具。不同的裂项方法适用于不同的函数和序列，在使用时需要根据具体的形式选择合适的方法。

案例 1：简单的裂项相消

考虑数列：

$$S=\sum _{n=1}^N(\frac{1}{n}-\frac{1}{n+1})$$

步骤：

1. 将每一项进行拆分：

   $$\frac{1}{n}-\frac{1}{n+1}$$

2. 累加后观察相消：

   $$S=(\frac{1}{1}-\frac{1}{2})+(\frac{1}{2}-\frac{1}{3})+\cdots +(\frac{1}{N}-\frac{1}{N+1})$$

3. 计算剩余项： 可以看到，除了第一个 $\frac{1}{1}$ 和最后一个 $-\frac{1}{N+1}$ 之外，其他项都相互抵消了。因此：

   $$S=1-\frac{1}{N+1}=\frac{N}{N+1}$$

案例 2：稍复杂的裂项相消

考虑数列：

$$S=\sum _{n=1}^N\left(\frac{1}{n(n+1)}\right)$$

步骤：

1. 将每一项进行拆分：

   $$\frac{1}{n(n+1)}=\frac{1}{n}-\frac{1}{n+1}$$

2. 累加后观察相消：

   $$S=(\frac{1}{1}-\frac{1}{2})+(\frac{1}{2}-\frac{1}{3})+\cdots +(\frac{1}{N}-\frac{1}{N+1})$$

3. 计算剩余项： 同样，除了第一个 $\frac{1}{1}$ 和最后一个 $-\frac{1}{N+1}$ 之外，其他项都相互抵消了。因此：

   $$S=1-\frac{1}{N+1}=\frac{N}{N+1}$$

字母裂项相消

对于字母形式的裂项相消，同样的原理可以应用。考虑：

$$S=\sum _{n=1}^N\left(\frac{a}{n(n+a)}\right)$$

步骤：

1. 将每一项进行拆分：

   $$\frac{a}{n(n+a)}=\frac{a}{a}(\frac{1}{n}-\frac{1}{n+a})=\frac{1}{n}-\frac{1}{n+a}$$

2. 累加后观察相消：

   $$S=(\frac{1}{1}-\frac{1}{1+a})+(\frac{1}{2}-\frac{1}{2+a})+\cdots +(\frac{1}{N}-\frac{1}{N+a})$$

3. 计算剩余项： 同样，除了第一个 $\frac{1}{1}$ 和最后一个 $-\frac{1}{N+a}$ 之外，其他项都相互抵消了。因此：

   $$S=1-\frac{1}{N+a}=\frac{N+a-1}{N+a}$$

总结

裂项相消法是一种有效的求和方法，特别适用于某些特殊形式的数列。在使用时，关键在于正确地拆分每一项，并观察相邻项的抵消情况，从而简化计算过程。