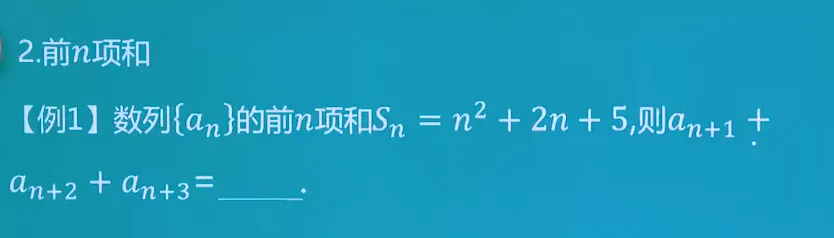什么是数列？

数列是一个按照一定规则排列的数的序列。在数学中，数列通常用来表示一个函数在自然数集上的取值。数列可以是有限的，也可以是无限的。

数列的基本概念

1. 定义：数列是一个由数构成的有序集合，通常用大写字母表示，例如 $(A,B,C)$ 等。
2. 项：数列中的每一个数称为数列的“项”。第 $(n)$ 项通常用 $(a_n)$ 表示。
3. 通项公式：数列的通项公式是用 $(n)$ 表示第 $(n)$ 项的表达式。

数列的类型

1. 算术数列：相邻两项之间的差是一个常数。例如：$(2,5,8,11,\dots )$ （公差为 3）。
2. 几何数列：相邻两项之间的比是一个常数。例如：$(3,6,12,24,\dots )$ （公比为 2）。
3. 递推数列：每一项依赖于前面的若干项。例如：斐波那契数列 $(0,1,1,2,3,5,8,\dots )$，其中每一项等于前两项之和。

数列的表示

数列可以用括号表示，如 $(a_1,a_2,a_3,\dots )$。对于无限数列，通常只写出前几项并加上省略号。

应用

数列在数学分析、数理统计、计算机科学等领域有广泛应用，特别是在求和、极限和级数等方面。

什么是通项公式？

通项公式是用来表示数列中第 $n$ 项的数学表达式。它允许我们通过给定的 $n$ 值直接计算出数列的任意一项，而无需列出所有前面的项。

通项公式的特点

1. 形式：通项公式通常表示为 $a_n$，其中 $n$ 是项的序号。例如，算术数列的通项公式可以表示为：

   $$a_n=a_1+(n-1)d$$

   其中 $a_1$ 是首项，$d$ 是公差。

2. 适用性：通项公式适用于各种类型的数列，包括算术数列、几何数列和递推数列等。

3. 计算：通过通项公式，可以快速计算出数列的任意项，而不需要逐项计算。

示例

• 算术数列：对于数列 $2,5,8,11,\dots$，通项公式为：

  $$a_n=2+(n-1)\cdot 3=3n-1$$

• 几何数列：对于数列 $3,6,12,24,\dots$，通项公式为：

  $$a_n=3\cdot 2^{n-1}$$

应用

通项公式在数学分析、数理统计和计算机科学等领域中非常重要，尤其是在求和、极限和级数等问题中。

求一个数列的通项公式通常可以通过以下几种方法进行：

1. 观察法

• 识别模式：观察数列的前几项，寻找规律。例如，检查是否是算术数列、几何数列或其他已知类型的数列。
• 例子：对于数列 $1,4,9,16,25,\dots$，可以观察到这些数是平方数，因此通项公式为 $a_n = n^2 $。

2. 差分法

• 计算差分：计算数列的第一差分（相邻项之差），如果第一差分是常数，则是算术数列；如果第一差分不是常数，继续计算第二差分，直到得到常数。
• 例子：对于数列 $1,3,6,10,15$：
  • 第一差分：$2,3,4,5$
  • 第二差分：$1,1,1$（常数）
  • 这表明这是一个二次数列，通项公式为 $a_n=\frac{n(n+1)}{2}$。

3. 递推关系

• 建立递推关系：如果数列的每一项可以通过前几项表示，可以建立递推关系，然后通过数学归纳法或其他方法求出通项公式。
• 例子：斐波那契数列 $F_n=F_{n-1}+F_{n-2}$，可以通过递推关系求出通项公式。

4. 拟合法

• 多项式拟合：如果数列的项数较多，可以使用多项式拟合的方法，假设通项公式为多项式形式，通过已知项求解系数。
• 例子：对于数列 $1,8,27,64$，可以假设 $a_n=A{n}^3+B{n}^2+Cn+D$，通过已知项求解 $A,B,C,D$。

5. 使用已知公式

• 查找已知数列：有些数列的通项公式是已知的，可以查阅相关文献或数据库（如OEIS）来找到对应的通项公式。