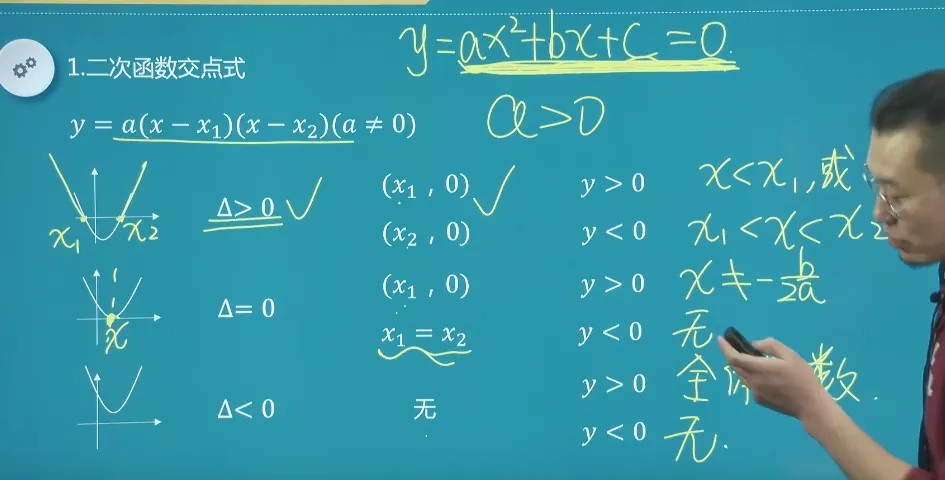
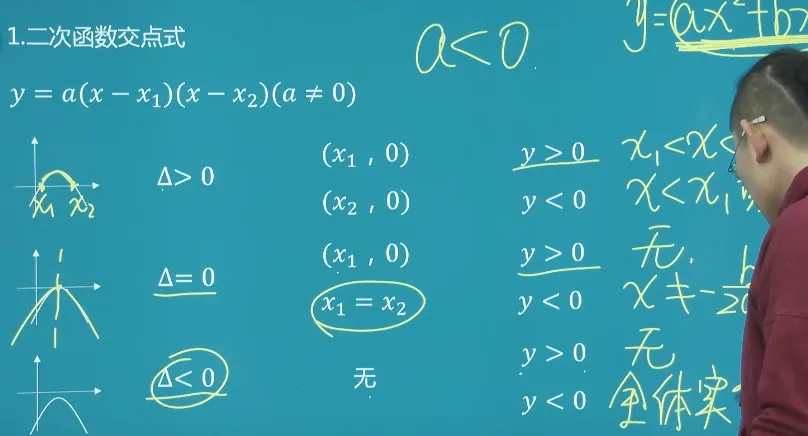
二次函数的交点式通常指的是二次函数与 $x$ 轴的交点，即求解方程 $(a{x}^2+bx+c=0)$ 的根。交点式可以表示为：

$$y=a(x-x_1)(x-x_2)$$

其中 $(x_1)$ 和 $(x_2)$ 是二次方程的两个根。

求解交点

1. 求根公式：对于方程 $(a{x}^2+bx+c=0)$，根可以通过求根公式得到：

$$x_{1,2}=\frac{-b\pm \sqrt{b^2-4ac}}{2a}$$

2. 交点式的形式：
   • 如果 $(D=b^2-4ac>0)$，则有两个不同的实根 $(x_1)$ 和 $(x_2)$。
   • 如果 $(D=0)$，则有一个重根 $(x_1=x_2)$。
   • 如果 $(D<0)$，则没有实根，二次函数与 $x$ 轴没有交点。

交点式的特点

• 交点：交点的 x 坐标为 $(x_1)$ 和 $(x_2)$，对应的 y 坐标为 0。
• 开口方向：与顶点式相同，开口方向由 $(a)$ 的符号决定。

示例

假设有一个二次函数 $(y=2x^2-4x+2)$，我们可以求出其交点：

1. 计算判别式：

$$D=(-4{)}^2-4\cdot 2\cdot 2=16-16=0$$

2. 计算根：

$$x_1=x_2=\frac{4}{4}=1$$

3. 交点式为：

$$y=2(x-1)(x-1)=2(x-1{)}^2$$

这表示该二次函数在 $(x=1)$ 处与 $x$ 轴相切。

一般式转换为交点式的作用

二次函数的交点式通常表示为：

$$y=a(x-x_1)(x-x_2)$$

其中 $(x_1)$ 和 $(x_2)$ 是二次函数与 x 轴的交点（即函数的根）。

一般式转换为交点式的作用：

1. 根的显式表示：交点式直接显示了二次函数的根 $(x_1)$ 和 $(x_2)$，便于分析函数的零点。

2. 图形理解：通过交点式，可以更直观地理解抛物线与 x 轴的交互关系，便于绘制图形。

3. 求解问题：在解决与根相关的问题（如求解方程、优化问题等）时，交点式提供了更直接的工具。

4. 因式分解：交点式便于进行因式分解，帮助简化计算和分析。

转换方法：

从一般式 $(y=a{x}^2+bx+c)$ 转换为交点式，可以通过求解方程 $(a{x}^2+bx+c=0)$ 找到根 $(x_1)$ 和 $(x_2)$，然后代入交点式。根的求解可以使用求根公式：

$$x_{1,2}=\frac{-b\pm \sqrt{b^2-4ac}}{2a}$$

这样就可以得到交点式。