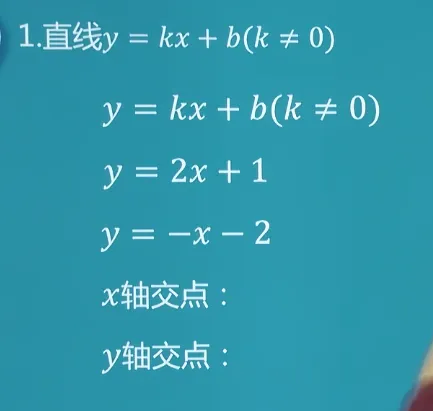
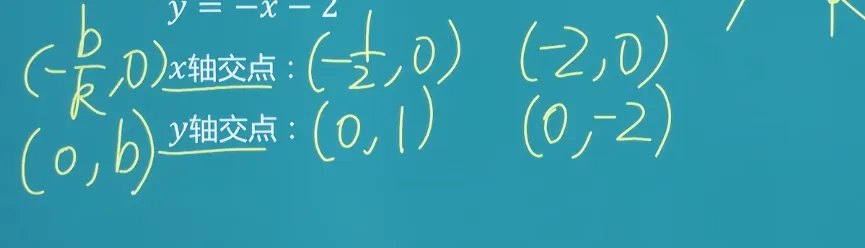
根据直线上的两点求直线的方程

为了求出线性方程 $y=kx+b$ 中的斜率 $k$ 和截距 $b$，我们需要已知的两点的坐标。假设这两点为 $(x_1,y_1)$ 和 $(x_2,y_2)$。

步骤：

1. 计算斜率k：

   $$k=\frac{y_2-y_1}{x_2-x_1}$$

2. 代入已知点求截距b： 使用其中一个已知点，例如 $(x_1,y_1)$，代入方程：

   $$y_1=k{x}_1+b$$

   变形得到：

   $$b=y_1-k{x}_1$$

示例：

假设已知点为 $(1,2)$ 和 $(3,4)$。

1. 计算k：

   $$k=\frac{4-2}{3-1}=\frac{2}{2}=1$$

2. 计算b： 代入点 $(1,2)$：

   $$b=2-1\cdot 1=1$$

最终结果：

因此，方程为：

$$y=1x+1\text{或简写为}y=x+1$$

求直线和抛物线的交点个数

要找直线和抛物线的交点个数，我们需要将直线方程和抛物线方程结合起来。假设直线方程为 $y=kx+b$，抛物线方程为 $y=a{x}^2+bx+c$。

步骤：

1. 设定方程： 将直线方程代入抛物线方程：

   $$kx+b=a{x}^2+bx+c$$

2. 整理方程： 将所有项移到一边，得到一个二次方程：

   $$a{x}^2+(b-k)x+(c-b)=0$$

3. 判别式： 对于二次方程 $A{x}^2+Bx+C=0$，其交点个数由判别式 $D=B^2-4AC$ 决定：

   • 如果 $D>0$，则有两个不同的交点。
   • 如果 $D=0$，则有一个交点（切点）。
   • 如果 $D<0$，则没有交点。

示例：

假设直线为 $y=2x+3$ 和抛物线为 $y=x^2-4$。

1. 代入方程：

   $$2x+3=x^2-4$$

2. 整理方程：

   $$x^2-2x-7=0$$

3. 计算判别式：

   $$D=(-2{)}^2-4\cdot 1\cdot (-7)=4+28=32$$

   由于 $D>0$，所以直线和抛物线有两个交点。